|
 4 4
|
 |
Концепция структурогенеза
[цикл из 16 статей] |
Волны химических реакций, среди которых особую известность получили волны БЖ, оказались неожиданными не только по своей природе. Как явствовало уже из первых осциллограмм, полученных Б. П. Белоусовым, они относились к особому классу — к классу уединенных волн или солитонов.
В настоящее время студенты ВУЗов изучают волновые процессы на примере синусоидальных колебаний, и лишь немногие из них получают теоретические представления о солитонах, которые являются единственным типом волн физиологических процессов. Уже изучая практические предметы, биологи и медики, не зная теории, сталкиваются с солитонами в виде нервных импульсов, волн сокращений миокарда, разрядов электрического ската, волн перистальтики, волн нервного возбуждения в тканях мозга и т.д. Поэтому есть смысл сказать несколько слов о солитонах вообще.
Физики и математики делят колебания на линейные и нелинейные. Теория линейных колебаний создана в XVIII-XIX веках и лежит в основе аппарата современной математической физики. Синусоидальные колебания — это линейные колебания. Систематическая теория нелинейных колебаний и волн — теория солитонов — появилась во второй половине XX века. Познакомиться с ней можно по работам [Филиппов, 1986; Додд и др., 1988; Ньюэлл, 1989] и многим другим.
Синусоидальные колебания в чистом виде — наиболее простые колебания, колебания одной определенной частоты, строго симметричные относительно исходного уровня. Для прохождения синусоидального колебания по каналам связи требуется минимальная ширина полосы частот. Все это обусловило широкое использование синусоидальных колебаний в технике, их почетное место в учебных программах.
Солитоны, как правило, распространяются в нелинейных средах, что существенно влияет на их особенности.
- Во-первых, нелинейность среды определяет некоторую оптимальную амплитуду солитона, от которой ему, в отличие от синусоидальных колебаний, труднее отклоняться и в меньшую, и в большую стороны.
- Во-вторых, нелинейность среды создает для него некую возможность обмена одних параметров на другие, скажем, амплитуды на форму. Последнее придает солитону способность распространяться без заметных изменений амплитуды на гораздо большие расстояния, чем мы ожидали бы по опыту работы с синусоидальными волнами.
- Наконец, в-третьих, нельзя не отметить, что нелинейность среды распространения солитонов часто определяется активностью среды и это особенно характерно для биологических тканей. В таких случаях размах и форма проходящего солитона имеют повышенную стабильность, потому что по мере движения солитона среда подпитывает его своей энергией.
Пожалуй, наиболее существенным свойством солитонов, резко отличающим их от синусоидальных колебаний, является независимость друг от друга. У синусоиды нельзя отделить одну волну от других или сдвинуть относительно других, изменить размах. Это сразу превратит синусоиду определенной частоты в нечто иное — в сложную совокупность разночастотных синусоидальных колебаний. Ничего похожего не грозит солитонам. Каждый из них можно, например, смещать во времени, и это не изменит ни его основных параметров, ни параметров других солитонов.
Соответственно, по отношению к солитонам нужно с большой осторожностью говорить о частоте. Они могут следовать на одинаковом расстоянии друг от друга (тогда обретает смысл понятие частоты следования), но могут от волны к волне резко изменять интервал или вовсе следовать через хаотически меняющиеся промежутки времени. В биологических процессах встречаются все эти случаи.
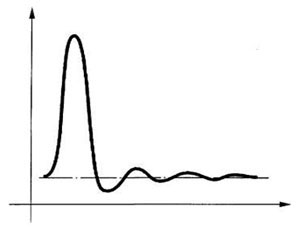 Типичная форма солитона показана на рисунке справа. Она может существенно изменяться в зависимости от природы процесса и параметров среды. Например, затухающие колебания за задним фронтом волны возникают только при существенном ухудшении условий прохождения высоких частот. Типичная форма солитона показана на рисунке справа. Она может существенно изменяться в зависимости от природы процесса и параметров среды. Например, затухающие колебания за задним фронтом волны возникают только при существенном ухудшении условий прохождения высоких частот.
Часто солитоны обладают большой скважностью, т.е. расстояние (во времени) между соседними волнами оказывается во много раз больше длительности самого колебания. В таких случаях энергия колебаний сосредотачивается на гораздо более высоких частотах, чем частота следования волн.
При резком различии скоростей процессов, определяющих передний и задний фронты волны, задний фронт может превратиться в медленно спадающую кривую, что придает солитону вид одиночного скачка параметра с последующим длительным (по сравнению с продолжительностью переднего фронта) возвращением в исходное состояние. Такую разновидность солитонов иногда называют кинками. Волны Белоусова-Жаботинского имеют именно такую форму — у них процессы, определяющие задний фронт волны, протекают намного медленнее, чем процессы, от которых зависит крутизна переднего фронта.
Способность солитонов следовать друг за другом через произвольные интервалы времени открывает для них большие возможности в части переноса информации. Кроме того, солитон, по сравнению с синусоидальными колебаниями, очень устойчив против возмущений, вносимых неоднородностью среды распространения и внешними помехами [Захаров, Шабат, 1962]. Эти свойства приобретают особую значимость при переносе информации в такой неоднородной и слабо защищенной от внешних воздействий среде, как живой организм.
Многие математики не согласны называть волны химических реакций солитонами. По их мнению, химические волны и солитоны — это разные понятия, разные категории объектов. Но в таком возражении проявляется лишь желание математиков подогнать понятие солитона под класс объектов, которые они научились описывать. Волны химических реакций они пока описывать не умеют. Между тем, многие специалисты вполне логично рассматривают солитон как нелинейное устойчивое локализованное возбуждение (например, [Шахбазов и др., 1996]), а такая трактовка охватывает и волны химических реакций.
Оптика нового типа
«Возможно такое, что вам и не снилось... Я буду рассказывать, как устроена Природа, и, если вам не понравится, как она устроена, это будет мешать вашему пониманию. Физики научились решать эту проблему: они поняли, что, нравится им теория или нет — неважно. Важно другое — дает ли теория предсказания, которые согласуются с экспериментом. Тут не имеет значения, хороша ли теория с философской точки зрения, легка ли для понимания, безупречна ли с точки зрения здравого смысла. Квантовая электродинамика дает совершенно абсурдное с точки зрения здравого смысла описание Природы. Но оно полностью соответствует эксперименту. Так что я надеюсь, что вы сможете принять Природу такой, какая она есть — абсурдной». © Фейнман, 1988
Сам факт осциллографической регистрации Б. П. Белоусовым химических колебаний показал, что в ходе реакции скачкообразно изменяется окислительно-восстановительный потенциал среды. Как оказалось, химической волне сопутствует скачок электрического потенциала порядка десятых или сотых долей вольта. Но есть ли основания считать, что подобные волны возникают в живых организмах?
Непосредственная регистрация в организме колебаний с ожидаемыми параметрами встречает серьезные технические трудности. Косвенные данные говорят, что длительность переднего фронта ожидаемых волн имеет временную протяженность порядка десятков пикосекунд. Это значит, что основная энергия колебаний сосредоточена в области десятков гигагерц. К тому же, мощность колебаний в расчете на одну клетку очень мала. Самые современные осциллографы еще не способны зарегистрировать подобные волны, показать их форму.
Учитывая, что увидеть осциллограмму структурогенных волн пока не удается, Герберт Пол заменил прямую регистрацию косвенными исследованиями на основе микродиэлектрофореза. В раствор, окружающий выделенную живую клетку, Пол ввел мельчайшие гранулы диэлектрика и наблюдал под микроскопом их поведение. В зависимости от того, у какого вещества — у жидкости или у гранул — была выше диэлектрическая проницаемость, частицы двигались к клетке, либо в противоположную сторону [Pohl, 1983]. Это четко указывало на существование в клетке переменного электрического поля. Но оставалось неясным, привязаны ли электрические колебания к поверхности клеток или же они протекают в объеме цитоплазмы?
На этот вопрос ответила другая серия опытов. Пол создал вокруг взвешенной в жидкости клетки вращающееся электрическое поле, и увидел, что клетка тоже стала вращаться, хотя и с меньшей скоростью. Более того, при изменении скорости вращения поля клетка обнаружила резонансные свойства — на определенных частотах она резко ускоряла свое вращение. Этот эффект, названный клеточным спиновым резонансом, противоречил предположению об электрических колебаниях на так называемой мембране, но говорил в пользу химических волновых процессов в протоплазме клетки.
Что произойдет при движении волны химических реакций в протоплазме клетки, когда фронт волны пересечет клеточное ядро?
В кольцевой зоне оболочки клеточного ядра, где в какой-то момент расположен скачок окислительно-восстановительного потенциала, возникнет очень высокая напряженность электрического поля. Скачок потенциала порядка десятых долей вольта воздействует на поверхностный слой (ошибочно называемый мембраной) общей толщиной всего 14 нм и создает в нем напряженность поля до 200 кВ/см. Вследствие этого в зоне соприкосновения фронта волны с ядерной оболочкой должно произойти интенсивное электрострикционное сжатие диэлектрического материала оболочки. Согласно расчетам [Артюшин, Барбараш, 1985], если бы отсутствовало гидравлическое сопротивление внутриядерной жидкости, то деформация оболочки достигла бы 10% диаметра ядра.
Быстрое перемещение кольцевой зоны деформаций по оболочке ядра порождает во внутриядерной жидкости акустические колебания. Скорости волн различной природы обычно не совпадают. Поэтому на границе раздела — на оболочке ядра, где энергия химических волн переходит в энергию акустических, происходит преломление волнового поля. Оболочка ядра является, в первом приближении, сферой. Явления, связанные с преломлением волнового поля на сферической поверхности, досконально изучены оптиками — такая поверхность приобретает свойства линзы. Конечно, того, что принято называть линзой, здесь нет. Но это не меняет результата. Возможно, следует ввести новый термин — линза-мембрана, мембролинза или что-либо в этом роде.
В обычной оптике преломляющиеся волны не изменяют свою природу в момент преломления, т.е. при переходе из области с одной скоростью распространения в область с другой скоростью. В обычной оптике изменение скорости распространения объясняется не изменением природы волнового поля, а изменением свойств среды распространения. Такую оптику можно условно назвать гомоволновой (homos — одинаковый). В нашем же случае изменение скорости вызывается именно изменением природы волнового поля. Здесь принципиально важно, что волны одной природы при достижении некой преобразующей пленки превращаются (передают свою энергию) в волны иной природы. Оптику этого неизвестного ранее типа можно назвать гетероволновой оптикой (heteros — иной, другой).
Гетероволновая оптика обладает рядом особенностей. Поскольку в ней могут сочетаться волновые процессы с сильно различающимися скоростями распространения, то оказываются достижимыми очень высокие коэффициенты преломления, а это позволяет при прочих равных условиях резко сократить количество компонентов оптической схемы и уменьшить аберрации. Если пленка-преобразователь работает на основе необратимого физического явления (например, в оболочке клеточного ядра возникает необратимая электрострикция, а не обратный пьезоэлектрический эффект), то из высокого коэффициента преломления не следуют, как это обычно бывает, высокие потери на отражение (так как не индуцируется противоволна). В гетероволновой оптике фокусирующими элементами служат не линзы, а тонкие пленки, из-за чего такая оптика имеет очень низкую материалоемкость.
Таким образом, оболочка ядра, действуя как линза гетероволновой оптики, преобразует химические волны протоплазмы в акустические колебания внутриядерной жидкости.
Термин «оптика» имеет два толкования — узкое и расширенное. В узком понимании это наука о том, что происходит с лучами видимой части спектра электромагнитных колебаний при их отражении, преломлении, поглощении и т.д. В расширенном понимании оптика охватывает процессы, в которых могут участвовать не только электромагнитные волны видимой части спектра, но и другие волны и объекты, поведение которых описывается сходными законами.
В расширенном понимании для разных конкретных задач термин «оптика» обычно дополняется уточняющим словом — «инфракрасная оптика», «рентгеновская оптика», «акустическая оптика», «электронная оптика», «оптика протонов» и т.д. Взаимодействие химических волн протоплазмы с клеточным ядром тоже описывается законами оптики, что дает основания отнести его к оптике в расширенном понимании. Соответственно, и здесь термин требует уточнения. Поскольку процессы связаны с ядром клетки, данный раздел оптики уместно назвать кариооптикой или сокращенно — К-оптикой.
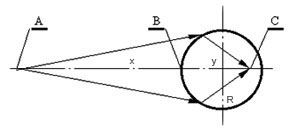 Представим себе, как показано на рисунке, что точка A относится к химическому волновому полю организма, т.е. находится вне ядра, а точка C является проекцией точки A в акустическом поле ядра. Эти точки расположатся на прямой, проходящей через центр ядра, и будут разделены ядерной оболочкой. Представим себе, как показано на рисунке, что точка A относится к химическому волновому полю организма, т.е. находится вне ядра, а точка C является проекцией точки A в акустическом поле ядра. Эти точки расположатся на прямой, проходящей через центр ядра, и будут разделены ядерной оболочкой.
Обозначим: R — радиус ядра; x — расстояние между точкой A и ближайшей точкой В на поверхности ядра; y — расстояние от точки В до точки фокусировки С; n — отношение скоростей распространения химических и акустических волн (коэффициент преломления).
Тогда, на основании формулы нулевого инварианта Аббе [Ландсберг, 1976] получим:
Анализ этой формулы, с учетом реальных размеров клеток животных и их ядер, показывает, что при n ≥ 2.7, все пространство организма, как бы велик он ни был, проецируется внутрь ядра каждой клетки [Артюшин, Барбараш, 1985]. Такой характер проекции не нарушается при изменениях размеров ядер.
Здесь мы столкнулись с явлениями, относящимися к химии, физике диэлектриков, теории нелинейных колебаний, оптике, биологии, а вовсе не к медицине. Именно поэтому до тех пор, пока проблемами здоровья человека будут заниматься именно медики, эту область естествознания будет окутывать полный мрак.

|